数学の勉強にやる気が出て好きになれるような面白いコツや式などはないでしょうか？

数学が楽しい！と感じられない、という点でお悩みなのですね。
今回は「1.数学の面白さが見える小話」と「2.数学という教科との向き合い方」の2つの視点でお答えします。

1.数学の面白さが見える小話

1-2.クラスに同じ誕生日の人がいるって、奇跡！？

30人ないし40人のクラスの中で、「誕生日が同じ2人がいた」という経験はありませんか？
「珍しい！」「運命だね！」などとクラスで話題になることもあるかもしれません。

それでは本当に、誕生日が同じ人がクラスにいた！というのは珍しいことだと思いますか？
実は、クラスに誕生日が同じ人が2人いることって、そこまで珍しいことではないのです。

なぜでしょう？
実際にクラスの人数をn人として、同じ誕生日の人が2人いる確率を求めてみましょう。

まず、全体から、n人の誕生日が全員バラバラである確率を引いて考えましょう(余事象の確率)。
n人に1～n番の番号付けをします。
1人目と2人目の誕生日が異なる確率は364/365、3人目とこれまでの2人の誕生日が異なる確率は363/365、4人目とこれまでの3人の誕生日が異なる確率は362/365......n人目とこれまでのn-1人の誕生日が異なる確率は(365-(n-1))/365。
これらをすべて掛け合わせると(364P(n-1))/365になり、これがn人の誕生日が全員異なる確率になります。
よって同じ誕生日の人が2人いる確率は全体からこれを引いた、
1-(364P(n-1))/365になります。

クラスの人数が30人だとして、この式にn=30を代入しますと、計算結果は0.706程度、すなわち30人学級の場合、約70%の確率で同じ誕生日の人がいる、ということが分かります。
なかなかの高確率だと思いませんか？

このように、珍しいと思っていたことでも、実際に確率を計算をしてみれば実はそこまで大したことではなかったということがあるかもしれません。

1-2.円周率は「3」なのか？「3.14」なのか？

皆さんは、小学校で円の直径・面積の求め方を学ぶときに、「円周率」というものを学んでいると思います。
そのとき学校で、「円周率は3.14ですよ」などと教わったことを覚えていることでしょう。

ところが実は2000年頃、国が、当時急速に進んだ「ゆとり教育」の流れに沿って、学習指導要領の改変に伴い「今後円周率は3と教えることにする」ことにした、という情報が流れたのです。
結果的にはこれは「学習指導要領上の記述の捉えようの問題」であり、必ず3と教えなければならないわけではなかった、ということが事実でした。
では、果たして円周率が3だと何がまずいのでしょうか？
下の図を見てください。

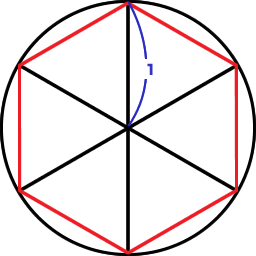
黒い太線は半径1の円とします。このときこの黒い太線で書かれた円の円周は1×2(直径)×3(円周率)=6となりますね。

一方赤線はこの円に内接した(頂点がすべて太線の円上)正六角形になります。
この正六角形は、隣り合う2頂点と円の中心の3点を結んでできる6つの正三角形からできています。
つまり、この正六角形の周の長さは1×6=6となるわけです。
しかしこれはおかしいですね。図で見ると明らかに長さは違うのに、このとき、「円の円周の長さ」と「その円に内接している正六角形の外周の長さ」が同じになってしまうのです。

これらを始め、多方向から多くの反発を招き、結果的には学習指導要領の次の改訂の際に、この部分の記述は書き換えられました。

ちなみに、この議論が熱を帯びていた2003年、東京大学の入試問題でこのような問題が出題されました。
「円周率が3.05よりも大きいことを証明せよ」
円周率が3であると教えさせようとしている国に対する東大からの警鐘だ！として話題になった問題です。

2.数学という教科との向き合い方

2-1.「授業」の重要性

数学の勉強をする際、学校の授業をないがしろにして、参考書だけを使って自力で勉強しようとする人がいます。
参考書には、数学の問題を解く上で頻出の様々な解法パターンが提示されていますので、それを読んで覚えようとしてしまいがちです。

ところが、参考書には「どうしてそのようなパターンで解くのか」を詳しくは載せてくれていません。
そのため、参考書で学んだパターンの存在を忘れてしまったり、覚えていても自分でうまく使いこなせなかったり...ということがよくあります。
実はその部分をしっかり説明してくれるのが「授業」の存在なのです。

今数学の得点が伸びず好きになれない...という人の中に、授業をないがしろにして自分で進めてしまっている人はいませんか？
しっかり授業に参加して、先生の話を聞くと、参考書で学んだことの理解を深められるかもしれませんよ。

2-2.「問題の読み替え」

では、数学の問題に対してどう向き合うべきか、についてお話ししましょう。皆さんは「問題の読み替え」を意識していますか？

「問題の読み替え」とは「その問題の答えを出すためには結局何を求められれば良いのか、を見つけること」です。
例を挙げて「△ABCの面積を求めよ」という問題で考えてみます。

まず、「△ABCの面積を求めるには何が必要なのか」を考えてください。
もしABとACの長さが分かっていれば、必要なのはどこでしょうか。
それは「sin∠BAC」です(高校の数学Ⅰという科目で学びます)。
つまり、この場合は「sin∠BACを求めよ」という問題に読み替えられるわけです。

ではその次は「sin∠BACを求めるためには何が必要か」を考えます。
もし4点A,B,C,Dが同一円周上にあったならば、円周角の定理が使え、さらにこの問題を「sin∠BDCを求めよ」に言い換えられるかもしれません。
このように、自分の知っている公式や定理、パターンを用いて問題をどんどん読み替えていき、容易に答えが分かる問題に変えることで、数学の問題に対して感じる複雑性はなくなるでしょう。
数学の問題に対する向き合い方についてお悩みの皆さんには、ぜひとも身につけていただきたい見方です。